En algunos casos es interesante considerar que X es pequeño frente a 1 y hacer las divisiones al revés, empezando por las constantes (que son los términos mayores) y terminando por los Xn, con n grande. Formalmente, se modifica la definición del grado: d o (Xn) = - n. La diferencia es que ya no hay unicidad, y es necesario fijarse por antelación una precisión, es decir un grado máximo al resto.
Por ejemplo, dividamos  por
por  al orden 3: el resto deber haber como término más fuerte (aquí el monomio de menor exponente) a lo mejor X4. La igualdad obtenida (en azul) equivale a:
al orden 3: el resto deber haber como término más fuerte (aquí el monomio de menor exponente) a lo mejor X4. La igualdad obtenida (en azul) equivale a:
 por
por  al orden 3: el resto deber haber como término más fuerte (aquí el monomio de menor exponente) a lo mejor X4. La igualdad obtenida (en azul) equivale a:
al orden 3: el resto deber haber como término más fuerte (aquí el monomio de menor exponente) a lo mejor X4. La igualdad obtenida (en azul) equivale a:
lo que, además de ser cierta, es un caso especial de la suma de términos de una sucecion geométrica:

y cada valor de n corresponde a una división euclidiana con una precisión distinta.
Otro punto de vista es considerar a  como el inicio del desarrollo de
como el inicio del desarrollo de  en serie de Taylor
en serie de Taylor
 como el inicio del desarrollo de
como el inicio del desarrollo de  en serie de Taylor
en serie de Taylor
Más generalmente, la serie de Taylor de una función racional se obtiene mediante la división euclidiana de la serie de Taylor del numerador por la del denominador. Por ejemplo, consideremos la función trigonométricatangente:  , y busquemos su desarrollo alrededor de 0 al orden 5. Hay que conocer las series al orden 5 (por lo menos) del seno y del coseno, y dividirlas descartando sistemáticamente los términos de orden mayor que aparecen en el cálculo. Como la función tangente es par, sólo hay tres monomios (en X, X³ y X5) que buscar. El resultado es
, y busquemos su desarrollo alrededor de 0 al orden 5. Hay que conocer las series al orden 5 (por lo menos) del seno y del coseno, y dividirlas descartando sistemáticamente los términos de orden mayor que aparecen en el cálculo. Como la función tangente es par, sólo hay tres monomios (en X, X³ y X5) que buscar. El resultado es 
 , y busquemos su desarrollo alrededor de 0 al orden 5. Hay que conocer las series al orden 5 (por lo menos) del seno y del coseno, y dividirlas descartando sistemáticamente los términos de orden mayor que aparecen en el cálculo. Como la función tangente es par, sólo hay tres monomios (en X, X³ y X5) que buscar. El resultado es
, y busquemos su desarrollo alrededor de 0 al orden 5. Hay que conocer las series al orden 5 (por lo menos) del seno y del coseno, y dividirlas descartando sistemáticamente los términos de orden mayor que aparecen en el cálculo. Como la función tangente es par, sólo hay tres monomios (en X, X³ y X5) que buscar. El resultado es 
La división euclidiana también existe en los anillos de polinomios de múltiples variable K[X,Y,Z...], donde hay varias maneras de definir el grado (parcial, total...) y otras tantas de proceder a la división.

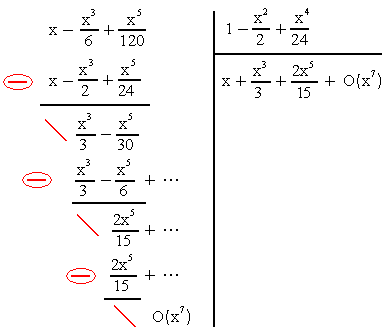
No hay comentarios.:
Publicar un comentario