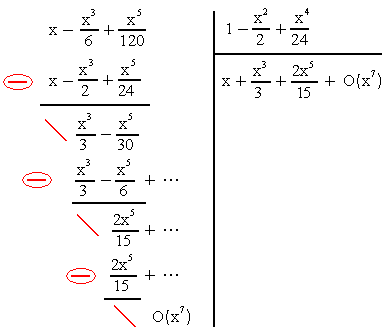DIVISIÓN DE POLINOMIOS

DIVISIÓN SEGÚN LAS POTENCIAS CRECIENTES

En algunos casos es interesante considerar que X es pequeño frente a 1 y hacer las divisiones al revés, empezando por las constantes (que son los términos mayores) y terminando por los Xⁿ, con n grande. Formalmente, se modifica la definición del grado: d ^o (Xⁿ) = - n. La diferencia es que ya no hay unicidad, y es necesario fijarse por antelación una precisión, es decir un grado máximo al resto.

Por ejemplo, dividamos $1$ por $1 - X$ al orden 3: el resto deber haber como término más fuerte (aquí el monomio de menor exponente) a lo mejor X⁴. La igualdad obtenida (en azul) equivale a:

$\frac {1 - X^4} {1 - X} = 1+ X + X^2 + X^3$

lo que, además de ser cierta, es un caso especial de la suma de términos de una sucecion geométrica:

$1+q+q^2 + ... + q^n = \frac {1-q^{n+1}} {1-q}$

y cada valor de n corresponde a una división euclidiana con una precisión distinta.

Otro punto de vista es considerar a $1 + X + X^2 + ... + X^n \$ como el inicio del desarrollo de $\frac {1} {1-X}$ en serie de Taylor

Más generalmente, la serie de Taylor de una función racional se obtiene mediante la división euclidiana de la serie de Taylor del numerador por la del denominador. Por ejemplo, consideremos la función trigonométricatangente: $\tan = \frac {\sin} {\cos}$ , y busquemos su desarrollo alrededor de 0 al orden 5. Hay que conocer las series al orden 5 (por lo menos) del seno y del coseno, y dividirlas descartando sistemáticamente los términos de orden mayor que aparecen en el cálculo. Como la función tangente es par, sólo hay tres monomios (en X, X³ y X⁵) que buscar. El resultado es $\tan x = x + \frac {x^3} {3} + \frac {2x^5} {15} + O(x^{7})$

La división euclidiana también existe en los anillos de polinomios de múltiples variable K[X,Y,Z...], donde hay varias maneras de definir el grado (parcial, total...) y otras tantas de proceder a la división.

DIVISIÓN DE POLINOMIOS

La división algebraica es la operación que consiste en hallar uno de los factores de un producto, que recibe el nombre de cociente dado el otro factor, llamado divisor, y el producto de ambos factores llamado dividendo.

De la definición anterior se deduce que el dividendo coincide con el producto del divisor por el cociente. Así por ejemplo, si dividimos , se cumplirá que

Si el residuo no fuera igual a cero, entonces:

Para efectuar una división algebraica hay que tener en cuenta los signos, los exponentes y los coeficientes de las cantidades que se dividen.

(+)÷(+)=+

(–)÷(–)=+

(+)÷(–)=–

(–)÷(+)=–

DIVISION DE UN MONOMIO POR OTRO

Para dividir dos monomios se divide el coeficiente del dividiendo entre el coeficiente del divisor y a continuación se escriben las letras ordenadas alfabéticamente, elevando cada letra a un exponente igual a la diferencia entre el exponente que tiene en el dividendo y el exponente que tiene en el divisor. El signo del cociente será el que corresponda al aplicar la regla de los signos. EJEMPLO:

Dividir

SOLUCIÓN: EJEMPLO:Dividir SOLUCIÓN: EJEMPLO:Dividir SOLUCIÓN: En ocasiones el cociente de dos monomios es fraccionario y, por consiguiente, la división propiamente dicha no puede efectuarse en los siguientes casos:

a)Cuando una letra está elevada a un exponente menor al que se halla elevada dicha letra en el divisor.

b)Cuando el divisor contiene alguna letra que no se halla en el dividendo.
EJEMPLO:Dividir

DIVISIÓN DE UN POLINOMIO POR UN MONOMIO

Para dividir un polinomio por un monomio se divide cada uno de los términos del polinomio por el monomio teniendo en cuenta la regla de los signos, y se suman los cocientes parciales así obtenidos.

EJEMPLO:

Dividir

SOLUCIÓN:

EJEMPLO:

Dividir

SOLUCIÓN:

EJEMPLO:

Dividir

SOLUCIÓN:

DIVISIÓN DE UN POLINOMIO POR UN POLINOMIO.

Para dividir dos polinomios se procede de la manera siguiente:

1) Se ordena el dividendo y el divisor con respecto a una misma letra.

2) Se divide el primer término del dividendo entre el primer término del divisor, obteniéndose así el primer término del cociente

3) Se multiplica el primer término del cociente por todo el divisor y el producto así obtenido se resta del dividendo, para lo cual se le cambia de signo y se escribe cada término de su semejante. En el caso de que algún término de este producto no tenga ningún término semejante en el dividendo, es escribe dicho término en el lugar que le corresponda de acuerdo con la ordenación del dividendo y del divisor.

4) Se divide el primer término del resto entre el primer término del divisor, obteniéndose de este modo el segundo término del cociente.

5) El segundo término del cociente se multiplica por todo el divisor y el producto así obtenido se resta del dividendo, cambiándole todos los signos.

6) Se divide el primer término del segundo resto entre el primer término del divisor y se repiten las operaciones anteriores hasta obtener cero como resto.

EJEMPLO:

Dividir:

Para resolver la operación anterior se procedió del modo siguiente:

En primer lugar se han ordenado dividendo y divisor en orden ascendente con respecto a la letra y y en orden descendente con respecto a la letra x.

A continuación se ha dividido el primer término del dividendo, , entre el primer término del divisor, , obteniéndose , por cada uno de los términos del divisor, obteniéndose como resultado , que se escribe debajo de los términos semejantes del dividendo cambiando los signos de todos los términos semejantes, obteniéndose como primer resto .

Después se ha dividido entre obteniéndose como cociente , que es el segundo término del cociente. Multiplicando por todos los términos del divisor que se obtiene como resultado , que se escribe debajo de los términos semejantes del primer resto cambiando los signos de todos sus términos para efectuar la resta.

A continuación se ha procedido a efectuar la reducción de términos semejantes, obteniéndose como segundo resto

Finalmente se ha dividido entre , obteniéndose como cociente . Multiplicando por todos los términos del divisor se obtiene como producto , que se escribe debajo de los términos semejantes del segundo resto cambiando los signos de todos lo términos para efectuar la resta. A continuación se ha procedido a efectuar la reducción de términos semejantes, obteniéndose como tercer resto 0, con lo cual queda acabada la división.